
上一篇題提到翻開近年的公開試題目,發現有很多題目都可以用一些DSE課程框架外的方法計算(俗稱out syllabus方法)。本篇就以2018年final boss 題目說起:

–節錄自DSE 2019
驟眼看沒有難度,正路的解答方法為:
設
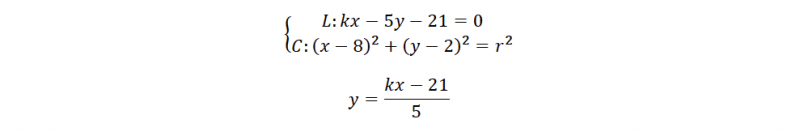
代L入C,可得:

由於L為該圓切線,圓與線只有一個交點,即:

方法雖然簡單但運算複雜,加上應考當日的緊張心情,要全取4分,的確要小心翼翼,而且會浪費不少塗改帶。
以前讀A. Maths 學過一條叫「點與線的距離式」(distance from a point to a line),點(x0,y0)與線 Ax+By+C=0 的距離可以於下列公式算出:
$$\ d=\frac{\left | Ax_{0}+By_{0}+C \right |}{\sqrt{A^{2}+B^{2}}}$$
用法簡單,只需要把點代進直線上,然後除以$$\sqrt{A^{2}+B^{2}}$$,計算結果如是負的話屈成正數便成(絕對值的關係)。
回說DSE題目,L: kx-5y-21=0 與圓心(8, 2)的距離,正正就是r。所以,套用距離公式:
$$\ r=\frac{\left | k(8)-5(2)-21 \right |}{\sqrt{k^{2}+5^{2}}}$$
要處理麻煩的絕對值,只須兩邊二次方就可解決:
$$\ r^{2}=\left ( \frac{8k-31}{\sqrt{k^{2}+25}} \right )^{2}$$
$$\ r^{2}=\frac{\left ( 8k-31\right )^{2}}{k^{2}+25}$$
只消兩三步,就已經做完,速度、穩定度完勝傳統方法。
大家如果想練一練這個方法,可以參照HKCEE制度的A. Maths教科書內的題目。

About Spencer Sir